Reglas de divisibilidad y calculadora de divisores
Contenido de esta página:
- Breve Introducción
- Conceptos Básicos (número divisible, divisor, primo y múltiplo)
- Calculadora online de los divisores de un número entero
- Reglas de Divisibilidad (del 1 al 15, del 25 y del 100)
- Algunas propiedades de divisibilidad
- Test online (Ejercicios)
Introducción
Las reglas de divisibilidad nos permiten saber, de forma más o menos rápida, si un número es divisible entre otro sin la necesidad de dividir.
Antes de empezar, recordamos los conceptos básicos que necesitamos:
Ejemplo: Podemos afirmar que el número 304050 es divisible entre 3 porque la suma de sus cifras es 12 (múltiplo de 3).
En esta página disponemos de una calculadora que proporciona los divisores (positivos) de un número entero y enumeramos las reglas de divisibilidad de los números del 1 al 15, del 25 y del 100 con ejemplos. También, enunciamos las propiedades básicas de divisibilidad y proporcionamos un test de 13 preguntas sobre la divisibilidad de números.Antes de empezar, recordamos los conceptos básicos que necesitamos:
Conceptos necesarios
Número divisible, divisor, primo y múltiplo.
Ver conceptos
Calculadora de números divisores
Calcular los divisores de .
Reglas de divisibilidad
A continuación, enumeramos las principales reglas o criterios de divisibilidad.
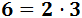
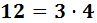
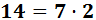
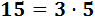 Por tanto, es divisible entre 15 si termina en 0 ó en 5 y, además, el resultado de la suma de sus cifras es múltiplo de 3.
Por tanto, es divisible entre 15 si termina en 0 ó en 5 y, además, el resultado de la suma de sus cifras es múltiplo de 3.
Divisible entre 1
Todo número es divisible entre 1.
Divisible entre 2
Si termina en 0, 2, 4, 6 ó 8.
Ver ejemplos
Divisible entre 3
Si la suma de sus cifras es múltiplo de 3.
A la hora de sumar, no es necesario sumar los 3’s.
Ver ejemplos
Divisible entre 4
Si sus dos últimas cifras son 00 ó un múltiplo de 4 (12, 16, 20, 24, 28, 32, 36 y 40).
Ver ejemplos
Divisible entre 5
Si termina en 0 ó en 5.
Ver ejemplos
Divisible entre 6
Si es divisible entre 2 y entre 3.
Ver ejemplo
Nota: para que un número sea divisible entre 6 tenemos que exigir que lo sea entre 2 y entre 3 porque podemos escribir 6 como:
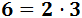
Divisible entre 7
En este caso tenemos un método más que una regla.
Ver método y ejemplo
Divisible entre 8
Si sus tres últimas cifras son 000 ó un múltiplo de 8 (104, 112, 120, 128,..., 992).
Ver ejemplos
Divisible entre 9
Si la suma de sus cifras es un múltiplo de 9 (9, 18, 27,...).
A la hora de sumar, no es necesario sumar los 9’s.
Ver ejemplo
Divisible entre 10
Si termina en 0.
Ver ejemplos
Divisible entre 11
Si la suma de las cifras que ocupan un lugar par menos la suma de las otras cifras es 0 ó un múltiplo de 11 (11, 22, 33, 44,…)
Ver ejemplo
Divisible entre 12
Si es divisible entre 3 y entre 4.
Ver ejemplo
Nota: para que un número sea divisible entre 12 tenemos que exigir que lo sea entre 3 y entre 4 porque podemos escribir 12 como:
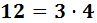
Divisible entre 13
Tenemos un método.
Ver método y ejemplos
Divisible entre 14
Si es divisible entre 7 y entre 2.
Ver ejemplos
Nota: hay que exegir la divisibilidad entre 2 y entre 7 porque podemos escribir 14 como el producto
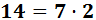
Divisible entre 15
Si es divisible entre 3 y entre 5.
Ver ejemplo
Nota: para que un número sea divisible entre 15 tenemos que exigir que lo sea entre 3 y entre 5 porque podemos escribir 15 como el producto
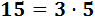
Divisible entre 25
Si termina en 00 ó en múltiplo de 25 (25, 50, 75).
Ver ejemplos
Divisible entre 100
Si termina en 00.
Algunas propiedades
Usaremos para representar que divide a , que es lo mismo que decir que es divisible entre ó que es un divisor de .
Nota: para no complicar las propiedades, suponemos que todos los números son positivos.
Nota: para no complicar las propiedades, suponemos que todos los números son positivos.
Ver propiedades y ejemplos
Test online
En todas las preguntas, escoger la única opción correcta.
Entonces...

Matesfacil.com by J. Llopis is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.
Pregunta 1
Los números 30, 45 y 36 son...
Divisibles entre 2 y entre 5.
| |
Divisibles entre 2 y entre 3.
| |
Divisibles entre 3 y entre 5.
|
Pregunta 2
Los números 3, 6, 9 y 12 son...
Divisibles entre 3.
| |
Divisibles entre 2 y entre 3.
| |
Divisibles entre 3 y entre 9.
|
Pregunta 3
Los números 60, 210, 330 son...
Divisibles entre 2, entre 7 y entre 10.
| |
Divisibles entre 2, entre 5 y entre 100.
| |
Divisibles entre 2, entre 3, entre 5 y entre 10.
|
Pregunta 4
Todos los números pares son...
Divisibles entre 2.
| |
Divisibles entre 4.
| |
Ninguna de las opciones anteriores es verdadera.
|
Pregunta 5
Todos los números impares son...
Divisibles entre 2.
| |
Divisibles entre 3.
| |
Ninguna de las opciones anteriores es verdadera.
|
Pregunta 6
El número 1176 es...
Divisible entre 2, entre 3 y entre 7.
| |
Divisible entre 2, entre 5 y entre 7.
| |
Divisible entre 2, entre 3 y entre 5.
|
Pregunta 7
Considerar los números 22, 333 y 132.
Todos son divisibles entre 11.
| |
El número 132 no es divisible entre 11.
| |
El número 333 no es divisible entre 11.
|
Pregunta 8
Todos los números cuyas dos últimas cifras son 28 son...
Divisibles entre 3.
| |
Divisibles entre 4.
| |
Divisibles entre 3 y entre 4.
|
Pregunta 9
Todos los números cuyas dos últimas cifras son 00 son...
Divisibles entre 3, entre 10 y entre 100.
| |
Divisibles entre 2, entre 4, entre 5, entre 10 y entre 100.
| |
Divisibles entre 2, entre 5, entre 7, entre 10 y entre 100.
|
Pregunta 10
El número 111111 es...
Divisible entre 11.
| |
Divisible entre 4 y entre 11.
| |
Divisible entre 3 y entre 4.
|
Pregunta 11
Si un número es divisible entre los números a y b (a y b son distintos), entonces...
Es divisible también entre el número a·b.
| |
No es divisible entre el número a·b.
| |
Ninguna de las opciones anteriores es verdadera, es decir, puede ser o puede no ser divisible entre a·b.
|
Ver razonamiento
Pregunta 12
Si un número es divisible entre los números primos a y b (a y b son distintos), entonces...
Es divisible también entre el número a·b.
| |
No es divisible entre el número a·b.
| |
Ninguna de las opciones anteriores es verdadera, es decir, puede ser o puede no ser divisible entre a·b.
|
Ver razonamiento
Pregunta 13
Tenemos un número cuyas cifras suman 9. Considerad todos los números que se obtienen al cambiar el orden de las cifras de dicho número.Entonces...
Todos los números que se obtienen reordenando sus cifras también son divisibles entre 3.
| |
No todos los números que se obtienen reordenando sus cifras también son divisibles entre 3.
|
Ver razonamiento
Reglas de divisibilidad - (c) - matesfacil.com

Matesfacil.com by J. Llopis is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.



No hay comentarios:
Publicar un comentario