En todos los ámbitos del conocimiento se pueden encontrar episodios de controversia a la hora de atribuir un descubrimiento o una invención. El mundo de las matemáticas no está, ni mucho menos, a salvo de ello. Quizás uno de los más conocidos es la invención del cálculo, con el enfrentamiento entre Newton y Leibniz. Otro ejemplo también muy famoso fue la resolución de la ecuación cúbica, es decir, la solución general de la ecuación
La historia de la resolución de la cúbica
En el año 1545 Girolamo Cardano publica Ars Magna, en el que presenta la solución general de la ecuación cúbica y la de la cuártica. Dicha publicación causó tal impacto en el mundo del álgebra que generalmente se considera el año 1545 como el que marca el período moderno en matemáticas. Pero, ¿fue Cardano el verdadero descubridor de los métodos de resolución de dichos tipos de ecuaciones?
Durante el siglo XV el dominio del álgebra estaba creciendo en Europa gracias a la difusión de los escritos procedentes de los árabes (grandes conocedores de esta rama). Mucha gente comenzó a estudiarla y muchos llegaron a dominarla tanto como para impartir clases sobre ella. Algunos métodos árabes se mejoraron en esta época y se añadieron nuevos casos y problemas. Pero el estudio de la ecuación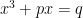 (escrita en forma moderna) seguía resistiéndose. Hasta había matemáticos, como Luca Pacioli, que aunque no decían que el problema no tenía solución sí lo comparaban con problemas tipo la cuadratura del circulo. .
(escrita en forma moderna) seguía resistiéndose. Hasta había matemáticos, como Luca Pacioli, que aunque no decían que el problema no tenía solución sí lo comparaban con problemas tipo la cuadratura del circulo. .
A mediados del siglo XVI, Niccolo Fontana, llamado Tartaglia por su condición de tartamudo, se trasladó a Venecia. Tartaglia llegó a ser famoso en la zona por sus trabajos realizados para los ingenieros del Arsenal veneciano.
Estando en la ciudad de los canales llegó a sus oídos que un tal Antonio Maria del Fiore presumía de conocer la fórmula maravillosa para resolver la ecuación cúbica. Dicha fórmula, según del Fiore, le había sido entregado por parte de un gran matemático 30 años antes. El hecho de que existiera alguna posibilidad de resolver la cúbica llevó a Tartaglia a trabajar en el desarrollo de un método de resolución, consiguiéndolo algo después.
A raíz de la noticia de este descubrimiento se organizó un desafío público entre del Fiore y Tartaglia. Aunque el primero de ellos era un matemático más bien mediocre, aceptó el desafío (puede que confiado por la fórmula maravillosa que poseía). Cada uno de ellos propuso 30 cuestiones al otro contendiente que tenían que ser resueltas en un tiempo concreto. Los de Tartaglia trataban sobre temas aritméticos, geométricos y algebraicos. Lo de del Fiore tenían todos la misma temática: ecuaciones cúbicas sin término de grado dos. Cuando llegó el día fijado para la presentación de las soluciones, Tartaglia había resuelto todos los problemas propuestos por del Fiore, pero éste no había podido dar respuesta a ninguna de las cuestiones propuestas por Tartaglia. Ni siquiera uno en el que se debía resolver una ecuación cúbica, para la que Tartaglia conocía un método particular.
La noticia del desafío y de la aplastante victoria de Tartaglia llegó a oídos de Cardano, que prometió buscarle alguien que lo patrocinara en el futuro (Tartaglia no tenía en aquella época ningún apoyo) a cambio de que le revelara el método de resolución de la cúbica, además de nombrarle en Ars Magna como descubridor de la misma. A pesar de estas promesas Tartaglia no accedió a compartir su tesoro con Cardano.
Pero la resistencia de Tartaglia no duró mucho. En 1539 Cardano invita a Tartaglia a pasar unos días con él en Milan y nuestro amigo Niccolo Fontana acaba cayendo: revela a Cardano los métodos de resolución de las tres formas en las que puede presentarse una ecuación cúbica sin término de segundo grado (a saber,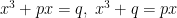 y
y  ) a condición de que éste no los publique.
) a condición de que éste no los publique.
Cardano comienza en ese mismo instante a estudiar la fórmula de Tartaglia junto con su ayudante Ludovico Ferrari. Poco después consigue resolver la cúbica en su forma general, es decir, de la forma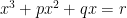 , reduciéndola mediante una transformación a uno de los tres tipos anteriores.
, reduciéndola mediante una transformación a uno de los tres tipos anteriores.
Pero había un pequeño problema: en ciertas ecuaciones que parecían normales aparecían soluciones en las que se podía encontrar una raíz cuadrada con radicando negativo (estas ecuaciones son las que más adelante se llamarían irreducibles). Teniendo en cuenta que, como hemos comentado antes, en esta época ni siquiera los números negativos estaban demasiado aceptados, la aparición de este tipo de soluciones se veía como algo bastante extraño.
Quizás por eso Cardano y Ferrari viajaron a Bolonia en 1542. En este punto de la historia es donde entra el gran héroe de este artículo: Scipione del Ferro. Él fue realmente quien encontró la fórmula de la resolución de la cúbica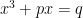 (Tartaglia también encontró métodos de resolución, pero se cree que dichos métodos no fueron descubiertos totalmente por él, sino que la idea provenía de alguna fuente anterior; de hecho se sabe que Tartaglia tendía a atribuirse ciertas publicaciones suyas cuando en realidad no lo eran). De hecho del Ferro fue el gran matemático que reveló a del Fiore (que era alumno suyo) la fórmula. También compartió su descubrimiento con Annibale della Nave, su propio yerno.
(Tartaglia también encontró métodos de resolución, pero se cree que dichos métodos no fueron descubiertos totalmente por él, sino que la idea provenía de alguna fuente anterior; de hecho se sabe que Tartaglia tendía a atribuirse ciertas publicaciones suyas cuando en realidad no lo eran). De hecho del Ferro fue el gran matemático que reveló a del Fiore (que era alumno suyo) la fórmula. También compartió su descubrimiento con Annibale della Nave, su propio yerno.
Durante el siglo XV el dominio del álgebra estaba creciendo en Europa gracias a la difusión de los escritos procedentes de los árabes (grandes conocedores de esta rama). Mucha gente comenzó a estudiarla y muchos llegaron a dominarla tanto como para impartir clases sobre ella. Algunos métodos árabes se mejoraron en esta época y se añadieron nuevos casos y problemas. Pero el estudio de la ecuación
A mediados del siglo XVI, Niccolo Fontana, llamado Tartaglia por su condición de tartamudo, se trasladó a Venecia. Tartaglia llegó a ser famoso en la zona por sus trabajos realizados para los ingenieros del Arsenal veneciano.
Estando en la ciudad de los canales llegó a sus oídos que un tal Antonio Maria del Fiore presumía de conocer la fórmula maravillosa para resolver la ecuación cúbica. Dicha fórmula, según del Fiore, le había sido entregado por parte de un gran matemático 30 años antes. El hecho de que existiera alguna posibilidad de resolver la cúbica llevó a Tartaglia a trabajar en el desarrollo de un método de resolución, consiguiéndolo algo después.
A raíz de la noticia de este descubrimiento se organizó un desafío público entre del Fiore y Tartaglia. Aunque el primero de ellos era un matemático más bien mediocre, aceptó el desafío (puede que confiado por la fórmula maravillosa que poseía). Cada uno de ellos propuso 30 cuestiones al otro contendiente que tenían que ser resueltas en un tiempo concreto. Los de Tartaglia trataban sobre temas aritméticos, geométricos y algebraicos. Lo de del Fiore tenían todos la misma temática: ecuaciones cúbicas sin término de grado dos. Cuando llegó el día fijado para la presentación de las soluciones, Tartaglia había resuelto todos los problemas propuestos por del Fiore, pero éste no había podido dar respuesta a ninguna de las cuestiones propuestas por Tartaglia. Ni siquiera uno en el que se debía resolver una ecuación cúbica, para la que Tartaglia conocía un método particular.
La noticia del desafío y de la aplastante victoria de Tartaglia llegó a oídos de Cardano, que prometió buscarle alguien que lo patrocinara en el futuro (Tartaglia no tenía en aquella época ningún apoyo) a cambio de que le revelara el método de resolución de la cúbica, además de nombrarle en Ars Magna como descubridor de la misma. A pesar de estas promesas Tartaglia no accedió a compartir su tesoro con Cardano.
Pero la resistencia de Tartaglia no duró mucho. En 1539 Cardano invita a Tartaglia a pasar unos días con él en Milan y nuestro amigo Niccolo Fontana acaba cayendo: revela a Cardano los métodos de resolución de las tres formas en las que puede presentarse una ecuación cúbica sin término de segundo grado (a saber,
Cardano comienza en ese mismo instante a estudiar la fórmula de Tartaglia junto con su ayudante Ludovico Ferrari. Poco después consigue resolver la cúbica en su forma general, es decir, de la forma
Pero había un pequeño problema: en ciertas ecuaciones que parecían normales aparecían soluciones en las que se podía encontrar una raíz cuadrada con radicando negativo (estas ecuaciones son las que más adelante se llamarían irreducibles). Teniendo en cuenta que, como hemos comentado antes, en esta época ni siquiera los números negativos estaban demasiado aceptados, la aparición de este tipo de soluciones se veía como algo bastante extraño.
Quizás por eso Cardano y Ferrari viajaron a Bolonia en 1542. En este punto de la historia es donde entra el gran héroe de este artículo: Scipione del Ferro. Él fue realmente quien encontró la fórmula de la resolución de la cúbica